1/9 x² + 2/3 xy +y² ∴
Answers
Answer:
Here is your ans. hope this helps you.

Related Questions
g(x) =2x + 4; Find g(-3)
Answers
Answer:
\(g(-3)=-2\)
Step-by-step explanation:
Substitute g(-3) into the function:
\(g(-3)=2(-3)+4\)
Multiply:
\(g(-3)=-6+4\)
Add:
\(g(-3)=-2\)
Answer: -2
Step-by-step explanation:
plug g(x) with -3 so it would be 2(-3) + 4 and then simply and add so 2(-3) equals -6 + 4 is -2
Show that Acos(?0t) + Bsin(?0t) can be written in the form r*sin(?0t - ?). Determine r and ? in terms of A and B. If Rcos(?0t - ?) = r*sin(?0t - ?), deermine the relationship among R, r, ? and ?.
r=
tan?=
R=
tan?*tan?=
Answers
To write Acos(?0t) + Bsin(?0t) in the form r*sin(?0t - ?), we can use the identities. The relationship among R, r, ? and ? is:
R^2 = r^2 (1 + (A/B)^2), tan? = r/R = B/A
r = sqrt(A^2 + B^2)
tan? = B/A
Therefore, r = sqrt(A^2 + B^2) and tan? = B/A.
To determine the relationship among R, r, ? and ?, we can use the identity:
R^2 = r^2 + (tan?)^2
Therefore, R = sqrt(r^2 + (tan?)^2) and tan? = r/R. Substituting the expression for tan? from earlier, we get:
tan? = B/A = r/R
Solving for R, we get:
R = r/tan? = r/(B/A) = rA/B
And substituting the expression for R in terms of r and tan?, we get:
R = sqrt(r^2 + (r/R)^2) * A/B
Simplifying this expression, we get:
R^2 = r^2 + (A/B)^2 * r^2
R^2 = r^2 (1 + (A/B)^2)
Therefore, the relationship among R, r, ? and ? is:
R^2 = r^2 (1 + (A/B)^2)
tan? = r/R = B/A
To show that Acos(ω₀t) + Bsin(ω₀t) can be written in the form r*sin(ω₀t - θ), we can use trigonometric identities. We know that:
sin(a - b) = sin(a)cos(b) - cos(a)sin(b)
Comparing this to the given expression, we have:
Acos(ω₀t) + Bsin(ω₀t) = r*sin(ω₀t - θ) = r[sin(ω₀t)cos(θ) - cos(ω₀t)sin(θ)]
Now, let's equate the coefficients of sin(ω₀t) and cos(ω₀t):
A = -r*sin(θ)
B = r*cos(θ)
To find r and θ in terms of A and B, we can use the Pythagorean identity:
A² + B² = (-r*sin(θ))² + (r*cos(θ))² = r²(sin²(θ) + cos²(θ)) = r²
Therefore, r = √(A² + B²).
Now, to find θ, we can use the tangent function:
tan(θ) = -A/B
Now, for the second part, if Rcos(ω₀t - θ) = r*sin(ω₀t - θ), we can use the sine-to-cosine transformation:
Rcos(ω₀t - θ) = Rsin(ω₀t - θ + π/2)
This implies that:
R = r
θ + π/2 = θ'
So, the relationship among R, r, θ, and θ' is:
R = r
θ' = θ + π/2
Learn more about sin at: brainly.com/question/19213118
#SPJ11
NEED HELP
Solve using elimination.
–8x − 4y = –20
8x + 5y = 13
Answers
Answer:
X=6 and y=-7
Step-by-step explanation:
A lawn company advertises that they can spread 7,500 square feet of grass seed in 2 and a half hours. Find the number of square feet of grass seed that can be spread per hour.
Answers
Answer:
3000 square feet
Step-by-step explanation:
Divide 7,500 by 2.5:
7500/2.5
= 3000
So, 3000 square feet of grass seed can be spread per hour
The owner of Britten's Egg Farm wants to estimate the mean number of eggs laid per chicken. A sample of 18 chickens shows they laid an average of 20 eggs per month with a standard deviation of 5 eggs per month.
(a-1) What is the value of the population mean?
20
It is unknown.
5
(a-2) What is the best estimate of this value?
Best estimate
(c)
For a 95% confidence interval, what is the value of t? (Round your answer to 3 decimal places.)
Value of t
(d)
Determine the 95% confidence interval for the population mean. is (Round your answers to 2 decimal places.)
Confidence interval to
(e-1) Would it be reasonable to conclude that the population mean is 17 eggs?
No
Yes
(e-2) What about 18 eggs?
Yes
No
Answers
(a-1) The value of the population mean is unknown.
(a-2) The best estimate of the population mean is the sample mean, which is 20 eggs.
(c) The value of t for a 95% confidence interval with 17 degrees of freedom is approximately 2.110.
(d) the 95% confidence interval for the population mean is approximately (17.902, 22.098).
(e-1) It would not be reasonable to conclude that the population mean is 17 eggs.
(e-2) It would be reasonable to conclude that the population mean is 18 eggs.
(a-1) The given information provides the sample mean (20 eggs) and the sample standard deviation (5 eggs), but it does not directly provide the population mean.
(a-2) In the absence of other information, the sample mean is a reasonable estimate of the population mean.
(c) For a 95% confidence interval, the value of t can be determined using the t-distribution with n-1 degrees of freedom, where n is the sample size. In this case, the sample size is 18, so the degrees of freedom is 18 - 1 = 17.
Using a t-distribution table or a statistical software, the value of t for a 95% confidence interval with 17 degrees of freedom is approximately 2.110.
(d) To determine the 95% confidence interval for the population mean, we can use the formula: Confidence interval = sample mean ± (t * standard error), where the standard error is the sample standard deviation divided by the square root of the sample size.
In this case, the sample mean is 20, the standard deviation is 5, the sample size is 18, and the value of t is 2.110. Plugging in these values, the confidence interval is 20 ± (2.110 * (5 / √18)), which evaluates to approximately 20 ± 2.098.
(e-1) The 95% confidence interval calculated in part (d) does not include 17 eggs, indicating that it is unlikely for the population mean to be 17 eggs.
(e-2) The 95% confidence interval calculated in part (d) includes 18 eggs, suggesting that it is plausible for the population mean to be 18 eggs.
For more such questions on population mean
https://brainly.com/question/31101410
#SPJ8
Dos números enteros suman 337 y su diferencia 43. ¿Cuál es el número mayor que hace cierta la premisa? AYUDA PORFA
Answers
Answer:
The largest number is 190.
Step-by-step explanation:
Given that,
Two whole numbers add up to 337 and their difference 43.
Let two whole number is x and y.
The sum of two whole number is
\(x+y=337\)
The difference of two whole number is
\(x-y=43\)
We need to calculate the numbers
Using equation (I) and (II)
\(x+y=337\)
\(x-y=43\)
Now, add the equations
\(2x=380\)
\(x=\dfrac{380}{2}\)
\(x=190\)
Put the value of x in equation (I)
\(190+y=337\)
\(y=337-190\)
\(y=147\)
The numbers are 190 and 147.
Hence, The largest number is 190.
need help with my math question 13
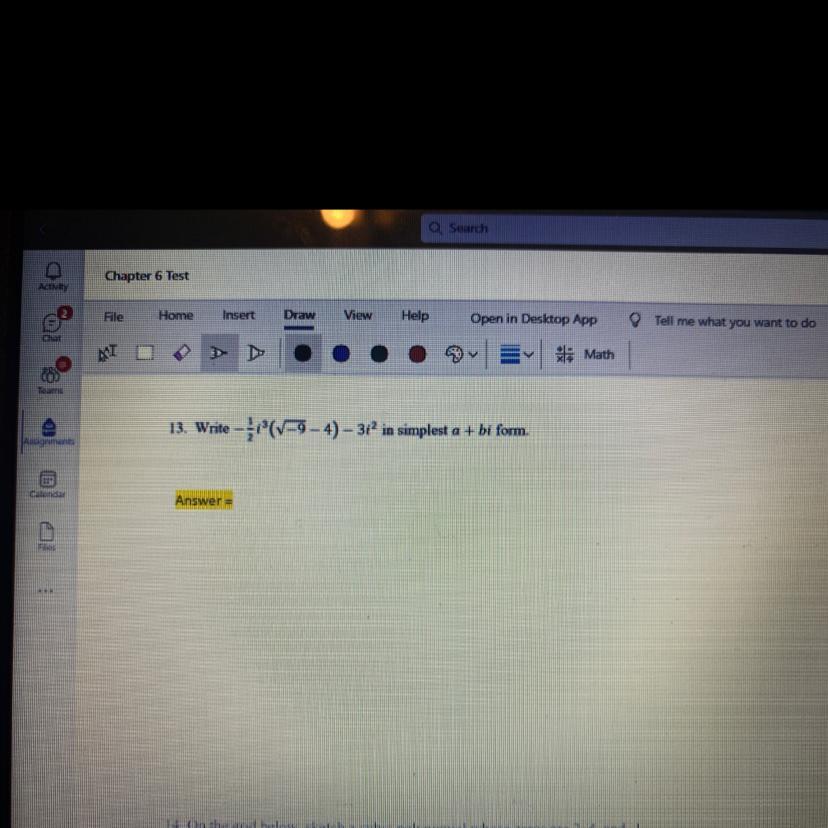
Answers
That's what I got for this question bro I'm not sure if I'm right
Step-by-step explanation:
\( \frac{3}{2} - 2i\)
Solve the system of equation using the elimination multiplication method 3c+6d=18
6c-2d=22
show your work
Answers
So the solution to the system of equations is:
c = 4, d = 1
What is equation?The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, separated by the 'equal' sign.
Define quadratic equation.x ax2 + bx + c = 0 is a quadratic equation, which is a second-order polynomial equation in a single variable. a 0. It has at least one solution since it is a second-order polynomial equation, which is guaranteed by the algebraic basic theorem.
Given equation I is \(3c+6d=18\) and equation II is \(6c-2d=22\)
We can start by multiplying the first equation by -2 and adding it to the second equation. This will eliminate the d variable:
\(-6c - 12d = -36\)
\(6c - 2d = 22\)
\(0c - 14d = -14\)
solving this we know value of \(d=1\)
So we know that d = 1, and we can substitute that into the first equation to find the value of c:
\(3c + 6d = 18\)
\(3c + 6(1) = 18\)
\(3c = 12\)
\(c = 4\)
So the solution to the system of equations is:
\(c = 4, d = 1\)
To know more about algebra visit:
https://brainly.com/question/24875240
#SPJ4
a bookshelf can hold a maximum of 45 books. let b represent the number of books to be shelved. which inequality represents how many books can be put the shelves? b>45
Answers
b < 45 represents the inequality of how many books can be put on the shelves.
An inequality is a mathematical statement that shows the relative size or ordering of two values. It is represented using symbols such as "<" (less than), ">" (greater than), "≤" (less than or equal to), "≥" (greater than or equal to), and "≠" (not equal to).
The inequality that represents how many books can be put on the shelves is:
b < 45
This inequality states that the number of books to be shelved, represented by b, must be less than 45 in order to fit on the bookshelf.
The inequality "b > 45" would represent a scenario in which the number of books to be shelved is greater than 45, which is not possible given the constraint that the bookshelf can hold a maximum of 45 books.
For more such questions on Inequality: brainly.com/question/28800558
#SPJ4
Point Q is the center of dilation. Triangles B prime C prime D prime and B C D are shown. The length of C prime Q is 3. The length of B prime C prime is 18. The length of D prime D is 2. The length of B D is 22 and the length of B C is 36. Angle B C D is 34 degrees and Angle B D C is 51 degrees. Triangle BCD was dilated using the rule D Subscript Q, one-half. What are the values of the unknown measures? m∠C'B'D' = ° CQ = B'D' =
Answers
Answer:
95 6 11
Step-by-step explanation:
im really smart lol jp :/
Answer:
m∠C'B'D' = 95
CQ = 6
B'D' = 11
Step-by-step explanation:
Edge2020
Have a great day! :)
a container of milk contains 8 cups of milk. if paul sets aside $1\frac{2}{5}$ cups of milk for use in a recipe and divides the rest evenly among his three children, how much milk should each child receive? express your answer as a mixed number.
Answers
Each child will receive the 1.1 cup of milk.
What is the unitary method?The unitary method is a method for solving a problem by the first value of a single unit and then finding the value by multiplying the single value.
Given that a container of milk contains 8 cups of milk. if paul sets aside \(1\dfrac{2}{5}\) cups of milk for use in a recipe , then we get the leftover;
8 - \(1\frac{2}{5}\) = 8 - 7/5
= 40- 7/5
= 33/5
= 6.6
The the rest cups of milk = 6.6
Then the rest evenly among his three children 6.6/3 = 1.1
Hence, Each child will receive the 1.1 cup of milk.
Learn more about the unitary method, please visit the link given below;
https://brainly.com/question/23423168
#SPJ1
How Many Intersections Are There Of The Graphs Of The Equations Below? 3x+30y = 36 None One Two Infinitely Many
Answers
The number of points of intersection for the graphs of the equations is infinite.
Point of intersection refers to the point at which two lines intersect on a graph. The graph of the equation refers to the visual demonstration of the equation obtained by plotting all the points of an equation on a graph. If there is only one variable, the graph is on a number line. If there are two variables, the graph is on the coordinate plane. If there are three variables, the graph is in three-dimensional coordinates.
Simplifying the given equations:
i) x/2 + 5y = 6
x + 10y = 12
ii) 3x + 30y = 36
3(x + 10y) = 36
x + 10y = 12
As the equations are equal lines, they will intersect at infinite times.
Note: The question is incomplete. The complete question probably is: How many intersections are there of the graphs of the equations below? x/2 + 5y = 6 3x + 30y = 36 none one two infinitely many
Learn more about Point of intersection:
https://brainly.com/question/11337174
#SPJ4
If x = -1, then which of the following inequalities makes a true statement?
A. -4x + 9 > 20
B. -4x – 5 < -15
C. -3x + 15 ≤ 18
D. -5x – 15 ≤ -22
Answers
Answer:
It is C
Step-by-step explanation:
Move all terms that don't contain x to the right side and solve.
When researcher uses his or her judgment or that of some other knowledgeable person to identify who will be in the sample, he or she is using what type of nonprobability sampling method
Answers
When a researcher uses his or her judgment or that of some other knowledgeable person to identify who will be in the sample, he or she is using the "Judgment Sampling" method of nonprobability sampling.
What is Judgment Sampling?Judgment sampling is a non-probability sampling approach in which a researcher or surveyor uses his or her own judgment or that of a qualified individual to select sample members. Judgment sampling is also known as purposive sampling because the researcher selects participants based on particular criteria.
The following are the characteristics of Judgment Sampling method:
The researcher identifies the sample by his or her own judgement.The sample is chosen based on the research question or goal, as well as the researcher's expertise or judgment.The sample participants are chosen from a group that the researcher considers representative of the population.The sample's size and representativeness are decided by the researcher's experience and judgment.In conclusion, when a researcher uses his or her judgment or that of some other knowledgeable person to identify who will be in the sample, he or she is using the Judgment Sampling method of nonprobability sampling.
Learn more about Judgment sampling here: https://brainly.com/question/30885091
#SPJ11
The optimal amount of x1, x2, P1, P2 and income are given by the
following:
x1= 21/ 7p1 x2= 51 / 7p2
The original prices are: P1=10 P2=5 The original income is: I
=4189 The new price of P1 is the foll
Answers
The total change in the consumed quantity of x₁ as per given price and income is equal to 213.
x₁ = (21/7)P₁
x₂ = (51/7)P₂
P₁ = 10
P₂ = 5
P₁' = 81
To calculate the total change in the quantity consumed of x₁ when the price of P₁ changes from P₁ to P₁',
The difference between the quantities consumed at the original price and the new price.
Let's calculate the quantity consumed at the original price,
x₁ orig
= (21/7)P₁
= (21/7) × 10
= 30
x₂ orig
= (51/7)P₂
= (51/7) × 5
= 36.4286 (approximated to 4 decimal places)
Now, let's calculate the quantity consumed at the new price,
x₁ new
= (21/7)P1'
= (21/7) × 81
= 243
x₂ new
= (51/7)P2
= (51/7) × 5
= 36.4286
The total change in the quantity consumed of x₁ can be calculated as the difference between the new quantity and the original quantity,
Change in x₁
= x₁ new - x₁ original
= 243 - 30
= 213
Therefore, the total change in the quantity consumed of x₁ is 213.
learn more about change here
brainly.com/question/32782775
#SPJ4
The above question is incomplete, the complete question is:
The optimal amount of x1, x2, P1, P2 and income are given by the following:
x1= 21/ 7p1 x2= 51 / 7p2
The original prices are: P1=10 P2=5 The original income is: I =4189 The new price of P1 is the following: P1'=81 Assume that the price of x1 has changed from P1 to P1'. What is the total change in the quantity consumed of x1?
Please answer step by step
A lighthouse sits at the edge of a cliff, as shown. A ship at sea level is 1100 meters from the base of the cliff. The angle of elevation from sea level to the base of the lighthouse is 48.1 degrees. The angle of elevation from sea level to the top of the lighthouse is 50.5 degress. Find the height of the lighthouse from the top of the cliff.
Do not round any intermediate computations. Round your answer to the nearest tenth.
Answers
We can use the tangent function to solve for the height of the lighthouse.
Let h be the height of the lighthouse from the top of the cliff.
tan(50.5 degrees) = (h + x) / 1100
tan(48.1 degrees) = h / 1100
We can divide the first equation by the second equation to get:
(h + x) / h = tan(50.5 degrees) / tan(48.1 degrees)
then we can simplify it by cross multiplying and canceling out h
h + x = (h * tan(50.5 degrees)) / tan(48.1 degrees)
then we can substract h from both sides
x = (h * tan(50.5 degrees)) / tan(48.1 degrees) - h
then we can substitute x = 1100
1100 = (h * tan(50.5 degrees)) / tan(48.1 degrees) - h
then we can add h to both sides
1100 + h = (h * tan(50.5 degrees)) / tan(48.1 degrees)
then we can multiply both sides by tan(48.1 degrees)
1100tan(48.1 degrees) + htan(48.1 degrees) = h * tan(50.5 degrees)
then we can divide both sides by tan(48.1 degrees)
h = (1100 * tan(48.1 degrees) + h * tan(48.1 degrees)) / tan(50.5 degrees)
after substituting the values we get:
h = (1100 * tan(48.1) + h * tan(48.1)) / tan(50.5)
we can round it to the nearest tenth
h = (1100 * tan(48.1) + h * tan(48.1)) / tan(50.5)
then we can use a calculator to get the exact number
h ≈ 191.5
Therefore, the height of the lighthouse from the top of the cliff is 191.5 meters.
chris has been given a list of bands and asked to place a vote. his vote must have the names of his favorite and second favorite bands from the list. how many different votes are possible?
Answers
There are nC2 different votes possible, where n is the number of bands on the list and nC2 represents the number of ways to choose 2 bands out of n.
To calculate nC2, we can use the formula for combinations, which is given by n! / (2! * (n-2)!), where ! represents factorial.
Let's say there are m bands on the list. The number of ways to choose 2 bands out of m can be calculated as m! / (2! * (m-2)!). Simplifying this expression further, we get m * (m-1) / 2.
Therefore, the number of different votes possible is m * (m-1) / 2.
In the given scenario, we don't have the specific number of bands on the list, so we cannot provide an exact number of different votes. However, you can calculate it by substituting the appropriate value of m into the formula m * (m-1) / 2.
Know more about factorialhere:
https://brainly.com/question/18270920
#SPJ11
you start a game with $60 in your wallet. you keep flipping a fair coin. if heads, you make $1 dollar, if tails, you loose 1$. you stop the game when you either have no money or you reach $100. what is the probability of being broke at the end of the game?
Answers
the probability of being broke at the end of the game is essentially 100%.
we can consider each coin flip as a separate event, with a probability of 0.5 for heads and 0.5 for tails. Let's calculate the probability of being broke at the end of the game.
First, we need to consider how many flips it would take to go from $60 to $0. If we keep losing $1 per flip, we would need to lose 60 times to reach $0. The probability of losing 60 times in a row is (0.5)^60, which is an extremely small number.
Secondly, we need to consider how many flips it would take to reach $100. If we keep winning $1 per flip, we would need to win 40 times to reach $100. The probability of winning 40 times in a row is (0.5)^40, which is also an extremely small number.
It is highly unlikely that someone would lose 60 times in a row, but it is still a possibility. As the number of flips increases, the probability of being broke becomes more and more certain.
In conclusion, while the probability of being broke at the end of the game is not exactly 100%, it is extremely close to that value.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
A numerical measure computed from a sample, such as sample mean, is known as a.
Answers
Answer:
Sample statistic
The spring concert at a certain high school sold 169 tickets. Students were charged â$6 each and adults â$8 each. The income from the sale of tickets was â$1192 . How many students and how many adults boughtâ tickets?
Answers
80 student tickets and 89 adult tickets were bought. Let x be the number of student tickets sold and y be the number of adult tickets sold. The sum of the two types of tickets is equal to the total number of tickets sold.
Let x be the number of student tickets sold and y be the number of adult tickets sold. The sum of the two types of tickets is equal to the total number of tickets sold. Therefore, x + y = 169 ...............(1)
The income from the sale of student tickets at $6 each is equal to 6x, and the income from the sale of adult tickets at $8 each is equal to 8y. Thus, the total income from the sale of tickets is:
6x + 8y = 1192 ................(2)
We have two linear equations: Equation (1) : x + y = 169
Equation (2) : 6x + 8y = 1192
We need to solve for x and y.
Step 1: We can multiply both sides of Equation (1) by 6 to eliminate x from Equation (2).
6x + 6y = 1014 (1a)
6x + 8y = 1192 (2)
Step 2: Subtract Equation (1a) from Equation (2).
2y = 178y = 89
Step 3: Substitute y = 89 into Equation (1) to find x.
x + 89 = 169x = 80
Therefore, 80 student tickets and 89 adult tickets were bought.
Answer: In this problem, the number of student tickets sold and the number of adult tickets sold have been found. Let x be the number of student tickets sold and y be the number of adult tickets sold. The sum of the two types of tickets is equal to the total number of tickets sold. Therefore, x + y = 169 ...............(1)
The income from the sale of student tickets at $6 each is equal to 6x, and the income from the sale of adult tickets at $8 each is equal to 8y. Thus, the total income from the sale of tickets is: 6x + 8y = 1192 ................(2)
We have two linear equations:
Equation (1) : x + y = 169
Equation (2) : 6x + 8y = 1192
We need to solve for x and y. We can multiply both sides of Equation (1) by 6 to eliminate x from Equation (2).
6x + 6y = 1014 (1a)
6x + 8y = 1192 (2)
We subtract Equation (1a) from Equation (2).
2y = 178y = 89
Therefore, the number of adult tickets sold was 89. Now, we substitute y = 89 into Equation (1) to find the number of student tickets sold. x + 89 = 169; hence, x = 80.
Therefore, 80 student tickets and 89 adult tickets were bought.
To know more about income visit:
https://brainly.com/question/2386757
#SPJ11
a diver was collecting water samples from a lake. he collected a sample at every 3m, starting at 5m below water surface. the final sample was collected at a depth of 35m.how many sample did he collected
Answers
The diver collected water samples at every 3 meters, starting from 5 meters below the water surface, up to a final depth of 35 meters.
We can find the number of samples collected by dividing the total depth range by the distance between each sample and then adding 1 to include the first sample.
The total depth range is:
35 m - 5 m = 30 m
The distance between each sample is 3 m, so the number of samples is:
(30 m) / (3 m/sample) + 1 = 10 + 1 = 11
Therefore, the diver collected a total of 11 water samples.
HELP!
Choose all that give the correct expression for the quantity described.
The difference of nine times a number x and the quotient of that number and 5.
9x − x over 5
Eight more than the quotient of twelve and a number n.
n over 12 + 8
The product of a number and the quantity ’six minus the number’ plus the quotient of eight and the number.
x(6 − x) + 8 over x
Sum of three consecutive even integers.2x + (2x + 2) + (2x + 4)
Answers
Answer:
did u ever get on answer cause I'm stuck in this too
Step-by-step explanation:
Catherine rolls a standard 6-sided die five times, and the product of her rolls is 300. How many different sequences of rolls could there have been
Answers
Catherine rolls a standard 6-sided die five times, and the product of her rolls is 300. The task is to determine the number of different sequences of rolls that could have resulted in this product.
To find the number of different sequences of rolls that could result in a product of 300, we need to consider the prime factorization of 300. The prime factorization of 300 is 2^2 * 3 * 5^2. Now, let's break down the problem into cases based on the number of factors of each prime number in the factorization.
1. Number of 2s: Since the prime factorization of 300 contains 2^2, there must be either 0, 1, or 2 rolls that resulted in a 2. This gives us three possibilities.
2. Number of 3s: The prime factorization contains 3^1, so there must be either 0 or 1 roll that resulted in a 3. This gives us two possibilities.
3. Number of 5s: The prime factorization contains 5^2, so there must be either 0, 1, or 2 rolls that resulted in a 5. This gives us three possibilities.
By multiplying the possibilities for each prime factor together (3 * 2 * 3), we find that there are 18 different sequences of rolls that could have resulted in a product of 300.
Learn more about sequence:
https://brainly.com/question/33469806
#SPJ11
A a supermarket sells the three bands of rice shown.

Answers
Answer:
the ansewr is b
Step-by-step explanation:
what is 2+2 i need help like rly bad i will give 100 points
Answers
Answer:
4 bestie <3
Step-by-step explanation:
Answer:
Step-by-step explanation:
4
(-3/4)x + 25 = (1/8)x - 3
Find x and show your steps.
Answers
Exclamation:
-3x\4+25=1/8x-3
-3/4x+25=x/8-3
-6x+200=x-24
200=x-24+6x
200=7x-24
200+24=7x
224=7x
224/7=32
Last month, Hoa's dog ate 40 cans of dog food in 31 days. How many cans should Hoa buy to feed his dog for the next 6 days?
Answers
Answer:
7.7419354839
Step-by-step explanation:
Explanation:
ok, so if Hao's dog ate 40 can's of dog food in 31 days, than therefore Hao's dog ate 4031 = 1.29 can's of dog food per day.
a set of values for the decision variables that satisfy all the constraints and yields the best objective function value is
Answers
A set of values for the decision variables that satisfy all the constraints and yields the best objective function value is a feasible solution that optimizes the objective function.
In optimization problems, decision variables are the quantities that we can control or adjust to achieve a desired outcome. Constraints are the limitations or conditions that these decision variables must satisfy. The objective function represents the goal or objective we want to optimize.
A feasible solution refers to a set of values for the decision variables that satisfy all the given constraints. This means that the solution meets all the specified requirements and does not violate any constraints. However, there can be multiple feasible solutions that meet the constraints.
Among these feasible solutions, the one that yields the best objective function value is the optimal solution. The objective function value is a measure of how well the solution aligns with the desired objective. The goal is typically to maximize or minimize this objective function value, depending on the problem.
To know more about objective function,
https://brainly.com/question/31841664
#SPJ11
Find the volume of the composite solid. Round to the nearest tenth, if necessary.

Answers
The volume of the composite figure with cone and hemisphere is 628 cubic inches
The given composite figure has a cone and hemisphere
Volume of cone =1/3πr²h
h is height of cone and r is radius of cone
h = 14 in and r is 5 in
Volume of cone = 1/3×3.14×5²×14
= 1/3×3.14×25×14
=1099/3 cubic inches
=366.3 cubic inches
Volume of hemisphere = (2/3)πr³
=2×3.14×5³/3
=785/3
=261.6 cubic inches
Total volume = 366.3 cubic inches + 261.6 cubic inches
=628 cubic inches
Hence, the volume of the composite figure with cone and hemisphere is 628 cubic inches
To learn more on Three dimensional figure click:
https://brainly.com/question/2400003
#SPJ1
Find the area of the region common to the interiors of the cardioids r = 1 + cosθ and r = 1 - cosθ. All work for every integral must be shown.
Answers
The area of the region common to the interiors of the cardioids r = 1 + cosθ and r = 1 - cosθ is (π + 2)/4.
We can find the area of the region common to the interiors of the cardioids by setting the two equations equal to each other and solving for θ. This will give us the values of θ that define the boundaries of the region. We can then integrate the area enclosed between the two curves over those boundaries.
1 + cosθ = 1 - cosθ
2cosθ = 0
cosθ = 0
θ = π/2, 3π/2
So the boundaries of the region are θ = π/2 and θ = 3π/2.
To find the area of the region, we can integrate the area enclosed between the two curves over these boundaries:
A = 2 ∫[0, π/2] (1 + cosθ) / 2 × dθ
Note that we multiply by 2 to account for the area in the other half of the region, between θ = 3π/2 and θ = 2π, which is symmetric.
Simplifying the integrand:
A = ∫[0, π/2] (1 + cosθ) / 2 × dθ
= (1/2) ∫[0, π/2] (1 + cosθ) dθ
= (1/2) (∫[0, π/2] dθ + ∫[0, π/2] cosθ dθ)
Evaluating the integrals:
A = (1/2) (θ ∣[0, π/2] + sinθ ∣[0, π/2])
= (1/2) (π/2 + sin(π/2) - 0 - sin(0))
= (1/2) (π/2 + 1)
= (π + 2) / 4
Learn more about the area of the region at
https://brainly.com/question/9485980
#SPJ4