10) The population of a particular country was 29 million in 1980; in 1985, it was 38 million. The exponential
growth function A = 29e^kt describes the population of this country t years after 1980. Use the fact that 5
after 1980 the population increased by 9 million to find k to three decimal places.
years
Answers
Answer: To three decimal places, k ≈ 0.052.
Step-by-step explanation: We are given the exponential growth function A = 29e^kt, where A is the population in millions t years after 1980.
In 1980, the population was 29 million, so A = 29 when t = 0. Substituting these values into the equation, we get:
29 = 29e^k(0)
29 = 29e^0
29 = 29
This confirms that the equation is true for t = 0.
In 1985, the population was 38 million, so A = 38 when t = 5. Substituting these values into the equation, we get:
38 = 29e^k(5)
Dividing both sides by 29, we get:
38/29 = e^5k
Taking the natural logarithm of both sides, we get:
ln(38/29) = 5k
Solving for k, we get:
k = ln(38/29) / 5 ≈ 0.052
Therefore, to three decimal places, k ≈ 0.052.
Related Questions
reword this plz The average test score for the science class after completing test 2 is 84.
Answers
Answer:
Given : The linear function f(x) = 0.2x + 79 represents the average test score in math class, where x is the number of the test taken.
The linear function g(x) represents the average test score in your science class, where x is the number of the test taken.
X
g(x)
1 1
86
2 3
84
82
To Find : test average for math class after completing test 2
test average for science class after completing test 2
Which class had a higher average after
completing test
Solution:
f(x) = 0.2x + 79
=> f/2) = 0.212) + 79 = 79.4f(x) = 0.2x + 79
=> f(4) = 0.2(4) + 79 = 79.8
test average for math class after completing test 4 = 79.8 =
1 1 2 3 4 g(x) 86 84 82 80
Х
g(2) = 84
test average for science class after completing test 2 = 84
g(4) = 80
test average for science class after completing test 4 = 80
80 > 79.8science class has more average than
MARK AS THE BRAINLIEST
math after 4 test
436,709 rounded to the nearest hundred thousand
Answers
Answer:
400,000
Step-by-step explanation:
The 10,000-meter long-distance running event in the summer Olympics is approximately 6.2 miles. Which equation could be used to determine the time, t, it takes to run 10,000 meters as a function of the average speed, s, of the runner where t is in minutes and s in miles per minute?
Answers
Answer:
\(\bold{t = f(s) = \dfrac{6.2}{s}}\)
Step-by-step explanation:
Given that distance is 10,000 meter or 6.2 miles.
Time taken is \(t\) minutes.
Average speed is \(s\) miles/minutes
To find:
Equation to determine time 't' as a function of average speed 's' = ?
t is in minutes and
s is in miles/minute
Solution:
First of all, let us have a look at the formula for Average Speed:
\(\text{Average Speed} = \dfrac{\text{Total Distance Traveled}}{\text{Total Time Taken}}\\\Rightarrow \text{Total Time Taken} = \dfrac{\text{Total Distance Traveled}}{\text{Average Speed}}\\\)
Now, we are given that Time, \(t\) should be in minutes and
Average speed, \(s\) must be in miles per minute
That means, we must have distance in miles.
Putting all the values in above formula.
So, the formula or equation becomes:
\(t = \dfrac{6.2}{s}\)
Therefore the equation to find time, \(t\) in minutes as a function of Average Speed, \(s\) is given as:
\(\bold{t = f(s) = \dfrac{6.2}{s}}\)
What is 8.7x0.45 if you multiply it
Answers
The solution to the multiplication of the decimals is; 39.15
How to multiply decimals?One of the ways to multiply decimals is as follows;
To multiply decimals, first multiply as if there is no decimal.
Second step is to count the number of digits after the decimal in each factor.
Last step is to put the same number of digits behind the decimal in the product.
Now, we want to multiply the decimals given as;
8.7 × 0.45
Converting them to fractions gives us;
(87/10) × (45/10)
= 3915/100
= 39.15
Thus, that is the solution to the multiplication of the decimals.
Read more about multiplying decimals at; https://brainly.com/question/28338004
#SPJ1
I need help pls I really need help it’s my little sisters homework

Answers
Answer:
25???
Step-by-step explanation:
determine the inclination of the following straight line
1. y=x+3 2) 3x-2y = 6
Answers
The inclination of the line represented by the equation y = x + 3 is 1, and the inclination of the line represented by the equation 3x - 2y = 6 is 3/2.
To determine the inclination (or slope) of a straight line, we can examine the coefficients of the variables x and y in the equation of the line.
The inclination represents the ratio of how much y changes with respect to x.
Equation: y = x + 3
In this equation, the coefficient of x is 1, which means that for every increase of 1 in x, y also increases by 1.
This indicates that the inclination of the line is positive, meaning it slopes upwards as x increases.
Since the coefficient of x is 1, the inclination can be expressed as 1/1 or simply 1.
Equation: 3x - 2y = 6
To determine the inclination, we need to rearrange the equation in slope-intercept form (y = mx + b), where m represents the slope.
First, isolate y:
-2y = -3x + 6
Divide the entire equation by -2 to solve for y:
y = (3/2)x - 3
Now we can observe that the coefficient of x is 3/2.
This indicates that for every increase of 1 in x, y increases by 3/2. Therefore, the inclination of this line is positive, indicating an upward slope.
The inclination can be expressed as 3/2.
For similar question on inclination.
https://brainly.com/question/29723347
#SPJ11
Can someone please actually solve this will mark brainlest and give five stars

Answers
In the circle the area of the shaded region and the length of arc ADB is 23/4 π and 23/6 π respectively.
What is length of arc?
The distance along the curved line that makes up the arc is measured using the arc length formula (a segment of a circle). The arc length is, to put it simply, the distance that passes through the curved line of the circle that forms the arc. It should be noted that the arc's length is greater than the separation of its ends along a straight line.
Given that the circle has a center O.
The radius of the circle is 3 yd.
The measure of ∠AOB is 130°.
First find the measure of ∠ADB -
∠ADB = 360° - ∠AOB
Substituting the values in the equation -
∠ADB = 360° - 130°
∠ADB = 230°
Now find the area of the shaded region.
The area of the shaded region can be determined using the formula -
A = (θ/360)πr²
Substituting the values in the equation -
A = (230/360) π(3)²
A = (230/360) π 9
A = 23/4 π or 5.75 π
Therefore, the area of the shaded region is 5.75 π yd².
Now, find the length of the arc ADB.
The length of arc ADB can be determined using the formula -
Arc Length = (θ/360)2πr
Arc Length = (230/360)2π3
Arc Length = 23/6 π or 3.83 π
Therefore, the length of arc is 3.83 π yd.
To learn more about length of arc from the given link
https://brainly.com/question/2005046
#SPJ1
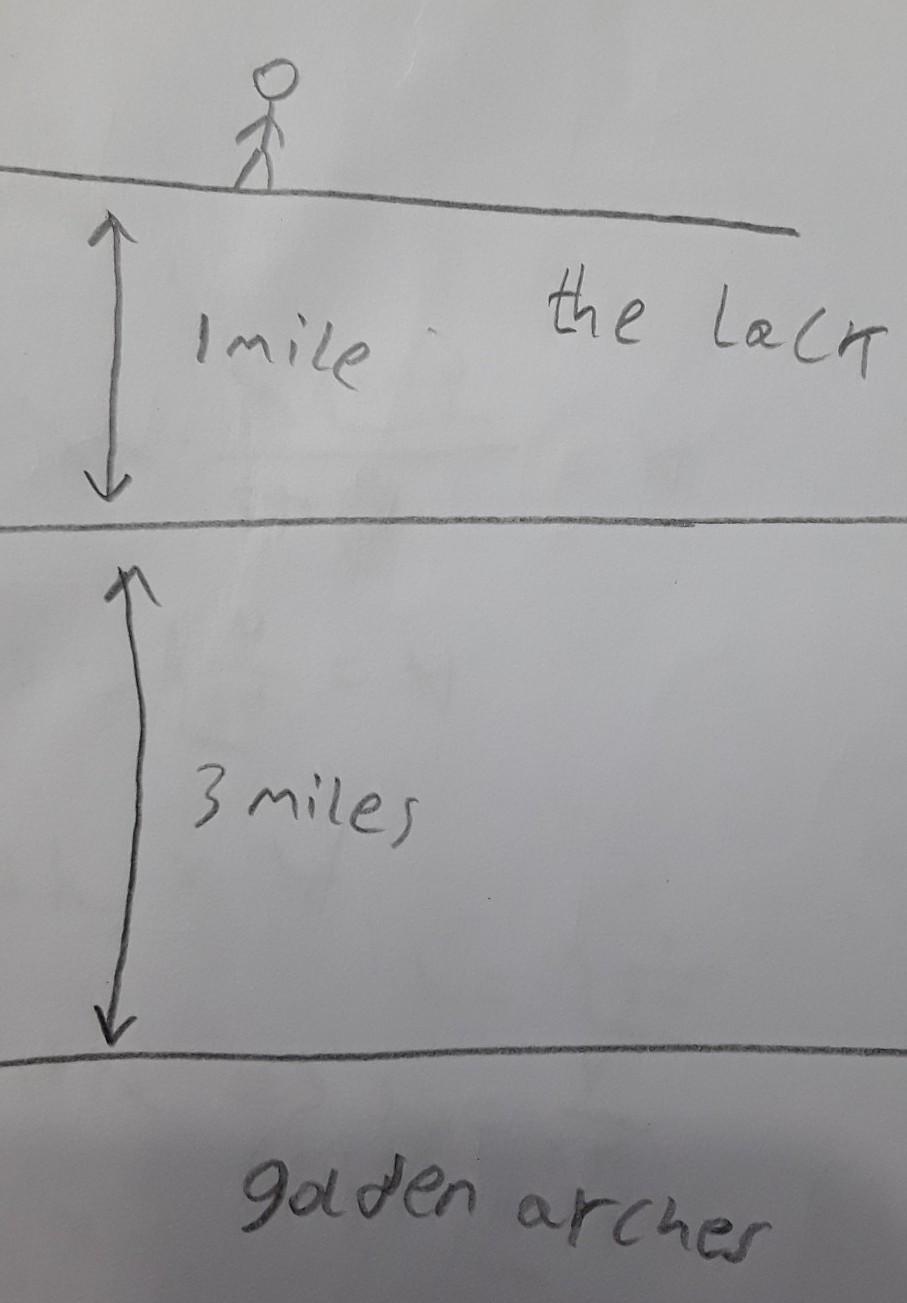
A boy standing on the shore of a lake 1 mile wide wants to reach the “Golden Arches” 3 miles down the shore on the opposite of the lake. If he swims at 2 mph and walks at 4 mph, is it quicker for him to swim directly across the lake and then walk to the Golden Arches or to swim directly to the Golden Arches? To the nearest minute, how much quicker?
Answers
Answer:
it is a matter of time
the speed is constant
use v=d/t
to find t and comparing it
Step-by-step explanation:
and in the 2nd case assume a cannel directly conects the land that boy stands on and the golden arches with the same distances
and note that the units are the same
Which steps are needed to solve this equation? . b + 6 = 21 Subtract 6 from both sides of the equation. The answer is b = 15. Check the solution by substituting 15 for b. Subtract 6 from the left side and add 6 to the right side of the equation. The answer is b = 27. Check the solution by substituting 27 for b. Add 6 to both sides of the equation. The answer is b = 27. Check the solution by substituting 27 for b. Add 6 to the left side and subtract 6 from the right side of the equation. The answer is b = 15. Check the solution by substituting 15 for b. edge
Answers
The solution by substituting 15 for b in the Original equation. The answer is true.
The steps needed to solve the equation b + 6 = 21 are:
Subtract 6 from both sides of the equation: b + 6 - 6 = 21 - 6, which simplifies to b = 15.
Check the solution by substituting 15 for b in the original equation: 15 + 6 = 21, which is true.
Therefore, the correct steps to solve the equation are:
Subtract 6 from both sides of the equation. The answer is b = 15
the solution by substituting 15 for b in the original equation. The answer is true.
To know more about Original .
https://brainly.com/question/27960093
#SPJ11
(Diversifying Portfolios MC)
worth points)
Name of Stock Symbol High Low Close
Stock A
105.19 103.25 103.38
Stock B
145.18 143.28 144.05
A
B
Last year, an investor purchase
difference in overall loss or ga
O The difference in overall gain is $207.00.
O The difference in overall loss is $207.00.
O The difference in overall loss is $200.70.
O The difference in overall gain is $200.70.
shares of stock A at $90 per share and 75 shares of stock B at $145 per share. What is the
ween selling at the current day's high price or low price?
Answers
The difference in overall gain between selling stock A at the current day's high price or low price and selling stock B at the current day's high price or low price is $239.50.
To determine the difference in overall gain or loss between selling stock A at the current day's high price or low price and selling stock B at the current day's high price or low price, we need to calculate the selling prices of the stocks.
Stock A:
High price = $105.19
Low price = $103.25
Close price = $103.38
Stock B:
High price = $145.18
Low price = $143.28
Close price = $144.05
The investor purchased 50 shares of stock A at $90 per share and 75 shares of stock B at $145 per share.
To calculate the selling prices, we need to multiply the number of shares by the respective selling price.
Selling price of stock A at the high price: 50 shares \(\times\) $105.19 = $5,259.50
Selling price of stock A at the low price: 50 shares \(\times\) $103.25 = $5,162.50
Selling price of stock B at the high price: 75 shares \(\times\) $145.18 = $10,888.50
Selling price of stock B at the low price: 75 shares \(\times\) $143.28 = $10,746.00
Now, let's calculate the difference in overall gain or loss:
Difference in overall gain = Selling price at the high price - Selling price at the low price
= ($5,259.50 + $10,888.50) - ($5,162.50 + $10,746.00)
= $16,148.00 - $15,908.50
= $239.50
For similar question on selling stock.
https://brainly.com/question/13454463
#SPJ8
PLEASE HELP! 40 points!!
3000 gallons of oil are to be transported to a destination 1000 miles away.
The only delivery truck available has a load capacity of 1000 gallons max. Additionally the truck consumes 1 gallon per mile from its load.
What is the maximum gallons of oil that can reach the destination when taking into account the truck consumption?
Answers
Answer:
0 gallon
Step-by-step explanation:
Given: 1 gallon per mile
total amount = 3000 gallons
capacity of truck = 1000 gallons
total number of trips = 3000/1000 = 3
total oil to reach the destination = 3000-3000=0
I hope this helps.
The maximum gallons of oil that can reach the destination when taking into account the truck consumption equals to zeroes.
What is Equation Modelling?Equation modelling is the process of writing a mathematical verbal expression in the form of a mathematical expression for correct analysis, observations and results of the given problem.
Given is 3000 gallons of oil are to be transported to a destination 1000 miles away. The only delivery truck available has a load capacity of 1000 gallons max. Additionally the truck consumes 1 gallon per mile from its load.
The maximum number of gallons of oil that can reach the destination when taking into account the truck consumption can be calculated as follows.
In one trip of 1000 miles, The amount of oil transferred will be -
1000 - 1 x 1000
0 Gallons.
Similarly, in all the trips the total gallons of oil reaching the destination will be zero.
Therefore, the maximum gallons of oil that can reach the destination when taking into account the truck consumption equals to zero gallons.
To solve more questions on Equation modelling, visit the link below-
https://brainly.com/question/18452531
#SPJ2
How many degrees are there in one radian?
Answers
Hope this helps :))
2. find all points of relative minima and maxima.

Answers
The relative maxima is at (0,1) and the relative minima are at (-1,0) and (1,0).
Now, For the relative minima and maxima of the function y = x⁴ - 2x² + 1, we need to take its first derivative and set it equal to zero to find the critical points.
So, the derivative of y with respect to x:
y' = 4x³ - 4x
Next, Put this derivative equal to zero and solve for x:
4x³ - 4x = 0
4x(x² - 1) = 0
This gives us critical points at x = 0, x = 1, and x = -1.
Now, we need to determine whether these critical points correspond to relative maxima or minima.
For this, we can use the second derivative test.
Taking the second derivative of y with respect to x:
y'' = 12x² - 4
Now, we can evaluate the second derivative at each critical point.
When x = 0, y'' = -4,
that's means that the critical point at x = 0 is a relative maximum.
When x = 1, y'' = 8,
That's means that the critical point at x = 1 is a relative minimum.
When x = -1, y'' = 8,
that's means that the critical point at x = -1 is also a relative minimum.
Hence, the relative maxima is at (0,1) and the relative minima are at (-1,0) and (1,0).
Learn more about the quadratic equation visit:
brainly.com/question/1214333
#SPJ1
Which one of the following is a unit vector?(A) <1, 1>(B)<1/2,1/2>(C)<3/5,4/5>(D) None of the above
Answers
Remmeber that
unit vector is a vector having magnitude of 1
so
Verify each option
(A) <1, 1>
magnitude^2=2 ------->magnitude=√2
is not a unit vector
(B)<1/2,1/2>
magnitude^2=(1/2)^2+(1/2)^2
magnitude^2=1/2 -----> magnitude=1/√2
is not a unit vector
(C)<3/5,4/5>
magnitude^2=(3/5)^2+(4/5)^2
magnitude^2=9/25+16/25
magnitude^2=25/25
magnitude=1
Is a unit vector
therefore
answer is option Cneed help real baddddddddddddd

Answers
Answer:
x≥2 and x<2 : ∅
x≥2 or x<2 : All real numbers
x≤2 and x≥2 : 2
Step-by-step explanation:
the first one must follow both conditions, so no number would work.
the second one works with any number, so all real numbers.
the third one has only one condition that works, 2
Please help if you can

Answers
1) The lower limit of the confidence Interval is: 1489.77.
The upper limit of the confidence Interval is: 1530.23
2) The lower limit of the confidence Interval is: 1478.32
The upper limit of the confidence Interval is: 15411.68
How to find the confidence Interval?The formula to find the confidence interval is:
CI = x' ± z(σ/√n)
where:
CI is confidence interval
x' is sample mean
z is z-score at confidence level
σ is standard deviation
n is sample size
1) The parameters are:
σ = $234
x' = $1510
n = 362
z at 90% CL = 1.645
Thus:
CI = 1510 ± 1.645((234/√362)
CI = 1510 ± 20.23
CI = (1489.77, 1530.23)
2) The parameters are:
σ = $234
x' = $1510
n = 362
z at 99% CL = 2.576
Thus:
CI = 1510 ± 2.576((234/√362)
CI = 1510 ± 31.68
CI = (1478.32, 15411.68)
Read more about Confidence Interval at: https://brainly.com/question/15712887
#SPJ1
6x-2=7x+9 find x plz help
Answers
Answer:
\(x=-11\)
Step-by-step explanation:
\(6x-2=7x+9\)
Add 2 to both sides:
\(6x-2+2=7x+9+2\)
\(6x=7x+11\)
Subtract 7x from both sides:
\(6x-7x=7x+11-7x\)
\(-x=11\)
Divide both sides by -1:
\(\frac{-x}{-1}=\frac{11}{-1}\)
\(x=-11\)
Answer:
X= -11
Step-by-step explanation:
Simplifying
6x + -2 = 7x + 9
Reorder the terms:
-2 + 6x = 7x + 9
Reorder the terms:
-2 + 6x = 9 + 7x
Solving
-2 + 6x = 9 + 7x
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-7x' to each side of the equation.
-2 + 6x + -7x = 9 + 7x + -7x
Combine like terms: 6x + -7x = -1x
-2 + -1x = 9 + 7x + -7x
Combine like terms: 7x + -7x = 0
-2 + -1x = 9 + 0
-2 + -1x = 9
Add '2' to each side of the equation.
-2 + 2 + -1x = 9 + 2
Combine like terms: -2 + 2 = 0
0 + -1x = 9 + 2
-1x = 9 + 2
Combine like terms: 9 + 2 = 11
-1x = 11
Divide each side by '-1'.
x = -11
Simplifying
x = -11
What is a dividend if the question is 1/2 divided by 1/4 =
Answers
Answer:
2
Step-by-step explanation:
Multiply the numerator of 1/2 with the denominator of 1/4 to get 4. Then multiply the denominator of 1/2 with the numerator of 1/4 to get 2. Lastly divide 4 by 2 to get 2.
Find the value of x for the following

Answers
Answer:
x = 13
Step-by-step explanation:
2(x + 18) and (3x + 79) are a linear pair and sum to 180° , that is
2(x + 18) + 3x + 79 = 180
2x + 36 + 3x + 79 = 180
5x + 115 = 180 ( subtract 115 from both sides )
5x = 65 ( divide both sides by 5 )
x = 13
Answer:
x = 13
Step-by-step explanation:
Given angles are,
→ 3x + 79°
→ 2(x + 18)° = 2x + 36°
Now we have to,
→ Find the required value of x.
We know that,
→ Sum of all angles in a line is 180°.
Forming the equation,
→ (3x + 79°) + (2x + 36°) = 180°
Then the value of x will be,
→ (3x + 79°) + (2x + 36°) = 180°
→ 3x + 79° + 2x + 36° = 180°
→ (3x + 2x) + (79 + 36)° = 180°
→ 5x + 115° = 180°
→ 5x = 180° - 115°
→ 5x = 65
→ x = 65/5
→ [ x = 13 ]
Hence, the value of x is 13.
The cross-section of this prism is a square with side length 4 m. What is the surface area of the prism?
(photo attached below.)

Answers
The final answer for the surface area of the prism is 32 m^2 + 16h m^2.
To find the surface area of the prism, we need to calculate the area of each face and sum them up.
The prism has two identical square faces and four rectangular faces. The square face has a side length of 4 m. The area of one square face is given by:
Area of square face = side length^2 = 4^2 = 16 m^2
Since there are two square faces, the total area of the square faces is:
Total area of square faces = \(2 * 16 = 32 m^2\)
The rectangular faces have a length equal to the side length of the square face (4 m) and a width equal to the height of the prism. Let's assume the height of the prism is h. The area of one rectangular face is given by:
Area of rectangular face = length * width = \(4 * h = 4h m^2\)
Since there are four rectangular faces, the total area of the rectangular faces is:
Total area of rectangular faces = \(4 * 4h = 16h m^2\)
Therefore, the surface area of the prism is the sum of the areas of the square and rectangular faces:
Surface area of prism = Total area of square faces + Total area of rectangular faces
= \(32 m^2 + 16h m^2\)
= \(32 m^2 + 16h m^2\)
The answer for the surface area of the prism is 32 m^2 + 16h m^2.
For more questions on prism
https://brainly.com/question/23963432
#SPJ8
Anwser The First 4 For ___ Points

Answers
Answer:
1) -2/3
2) 7/60
3) -11/10
4) 37/24
Step-by-step explanation: calculator
Answer:
1.= -2/10 2.298143
step-by-step explanation:
ansver
Answer from: Quest
step-by-step explanation:
x^2 -12x + 36 + y^2 = 36
x^2 + y^2 = 12x
r^2 = 12rcos(theta)
r = 12 cos(theta)
Step-by-step explanation:
What number when multipled by 1 1/3 has a product of 1
Answers
Answer: 3/4
.........................
An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division.
The number when multiplied by 1 1/3 has a product of 1 is 3/4.
What is an expression?An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division.
Example:
5 + 3x is an expression.
5x = 1/2 is an expression.
We have,
Number = M
The number when multiplied by 1 1/3 has a product of 1.
This can be written as:
M x \(1\frac{1}{3}\) = 1
\(1\frac{1}{3}\) = 4/3
So,
M x 4/3 = 1
Multiply both sides by 3/4.
M x 4/3 x 3/4 = 1 x 3/4
M = 3/4
Thus,
The number when multiplied by 1 1/3 has a product of 1 is 3/4.
Learn more about expressions here:
https://brainly.com/question/10978794
#SPJ2
Which equation can be used to solve for � xx in the following diagram?

Answers
Equation which can be used to solve for the value of x is
3x° + 2x° + 80 °= 180° .
Straight angle pair is the sum of two or more angles that are in pair of angles that form a straight line is always equal to 180°.
As shown in the diagram angle on the lines are -
3x ° , 80° , 2x° respectively
Sum of all these angle will be equal to 180°.
3x° + 2x° + 80° = 180
The correct equation to find the value of x is 3x° + 2x° + 80° = 180° .
To know more about equation click here :
https://brainly.com/question/31086219
#SPJ1
- 200
Solve it i need help

Answers
Answer:
\(-10\sqrt{2}\)
Step-by-step explanation:
\(-\sqrt{200}\)
To factor an integer, we need to repeatedly divide it by the ascending sequence of primes (2, 3, 5)
In the end, the number of times each prime divides the original integer becomes its exponent.
Prime number 2 to the power of 3 equals 8, and 5 to the power of 2 equals 25.
\(-\sqrt{2^{3}*5^{2} }\)
We need to rewrite certain factors as the product of two factors in order to remove them from the radical.
The exponent of the first factor in such a product will be equally divided by the radical index, allowing us to eliminate it from the radical.
Here, because their exponents are evenly divided by the radical index, we will be able to eliminate the following components from the radical:
\(2^{2}\) and \(5^{2}\)
\(-\sqrt{2^{2} *2*5^{2} }\)
\(-10\sqrt{2}\)
OAmalOHopeO
S see Use the graph y=e^x to evaluate these expression e^0

Answers
Answer:
\( y= e^x\)
And we want to evaluate e^0 using the graph
And as we can see in the plot the y intercept is the blue point with y=0 and that correspond with:
\( y(0)= e^0 =1\)
Step-by-step explanation:
For this problem we know the following function:
\( y= e^x\)
And we want to evaluate e^0 using the graph
And as we can see in the plot the y intercept is the blue point with y=0 and that correspond with:
\( y(0)= e^0 =1\)
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
Simplify (2s+5-3s)+4(s-6^2)
Answers
Answer: 3s-139
Step-by-step explanation: (2s+5 - 3s)+4(s-6^2)
Collect like terms and evaluate
(-s+5) +4 (s-36)
Rewrite and remove the parentheses
-S+5 +4s -144
Collect like terms and calculate and you get
3s-149
A lady borrows #2,000,000 to buy a land, she is charged compound interest at 9% per annum. she repays #1,280,000 after one year. How much should she repay at the end of the second year to clear her debt?
Answers
Using the concept of compound interest, the total amount she needs to pay is 2261000
What is compound interest?Compound interest is the interest calculated on the principal and the interest accumulated over the previous period. It is different from simple interest, where interest is not added to the principal while calculating the interest during the next period.
The formula is given as;
\(A = P(1 + \frac{r}{n})^n^t\)
A = Compounded InterestP = principalr = rate n = number of times compoundedt = number of yearsWe can calculate the interest in the first year;
Interest = Principal amount * Interest rate
Interest = 2000000 * 0.09 = 180,000
This is the sum of the loan, the interest of first year minus the lump sum after one year.
Remaining debt after the first year = 2,000,000 + 180,000 - 1,280,000 = 900,000
We can calculate the interest at the second year as;
Interest = 900000 * 0.09 = 81000
When we can the sum of everything to determine how much she needs to pay to clear her loan;
81000 + 900000 + 1280000 = 2,261,000
Learn more on compound interest here;
https://brainly.com/question/28020457
#SPJ1
Below is a frequency distribution from a random sample of the number of interceptions thrown in a football game by one quarterback. Frequency Distribution: Number of Interceptions Thrown in a Game Number of Interceptions Count Cumulative Count Percent Cumulative Percent 0 40 40 20% 20% 1 80 120 40% 60% 2 48 168 24% 84% 3 20 188 10% 94% 4 8 196 4% 98% 5 4 200 2% 100% a. How many observations are in the sample
Answers
Answer: 200
Step-by-step explanation:
No___count ____cumm____count%___cumm%
0_____40_______40_______20%_____20%
1_____80_______120_______40%_____60%
2____48________168_______24%_____84%
3____20________188_______10%______94%
4____8_________196_______4%_______98%
5____4_________200_______2%______100%
Hence number of observations in the sample is the sum of counts of each interception, which is also the bottom most value of the cumulative frequency column.
Sum of counts (40 + 80 + 48 + 20 + 8 + 4) = 200
Rewrite the following equations in the form (x−p)2=q 0=x^2-18x+1 and the equation x^2+26x+167.5=0
Answers
For the first equation, we can complete the square to find its vertex form. Here's how we do it:
0 = x^2 - 18x + 1
0 = (x - 9)^2 - 80
So we have (x - 9)^2 = 80. This is in the form (x - p)^2 = q, where p = 9 and q = 80.
For the second equation, we can complete the square in a similar way:
x^2 + 26x + 167.5 = 0
x^2 + 26x = -167.5
x^2 + 26x + (26/2)^2 = -167.5 + (26/2)^2
(x + 13)^2 = 9.25
So we have (x + 13)^2 = 9.25. This is in the form (x - p)^2 = q, where p = -13 and q = 9.25.
I hope that helps!