1) find a div m and a mod m when
a) a= -111, m = 99
b) a= -9999, m= 101
c) a= 10299, m=999.
d) a= 123456, m= 1001.
2) find the value of ( 893 mod 79)4 mod 26
Answers
a) Using the formula a = q * m + r, we have:
-111 = (-2) * 99 + 87
Therefore, a div m = -2 and a mod m = 87.
b) Using the same formula:
-9999 = (-99) * 101 + 12
So, a div m = -99 and a mod m = 12.
c)
10299 = 10 * 999 + 369
Thus, a div m = 10 and a mod m = 369.
d)
123456 = 123 * 1001 + 733
Therefore, a div m = 123 and a mod m = 733.
We can solve this by using the modulo arithmetic property that states that (a^b) mod m = ((a mod m)^b) mod m. Applying this property, we have:
(893 mod 79)4 mod 26 = (12^4) mod 26 = 20736 mod 26 = 8. Therefore, (893 mod 79)4 mod 26 = 8.
Visit here to learn more about formula brainly.com/question/20748250
#SPJ11
Related Questions
select the compound inequality shown on the graph.

Answers
A page in an average newspaper has 8 columns of print. Each column consists of 160 lines and each line averages 6 words. What's the average number of words on a full page?
Answers
Answer:
7,680
Step-by-step explanation:
A page has 8 columnsEach column consists of 160 lines.Each line averages 6 words.The average number of words on a full page
=Number of columns X Number of Lines X Number of words per line
=8 X 160 X 6
=7680
The average number of words on a full page is 7,680.
Evaluate the formula t=
x−μ
s
n when μ=117, n=28, x=113, and

Answers
Work Shown:
\(t = \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\\\\t = \frac{113-117}{\frac{11}{\sqrt{28}}}\\\\t \approx \frac{-4}{\frac{11}{5.291503}}\\\\t \approx \frac{-4}{2.078804}\\\\t \approx -1.924183\\\\t \approx -1.924\\\\\)
In the intermediate steps, I rounded to 6 decimal places. The final answer is rounded to 3 decimal places (to the nearest thousandth).
Which of the following pairs of correlation coefficients most closely corresponds to the observed correlations between the intelligence scores of adopted children and those of their adoptive or biological parents?
a. child-adoptive: 0.20; child-biological: 0.40
b. child-adoptive: 0.40; child-biological: 0.40
c. child-adoptive: 0.20; child-biological: 0.20
d. child-adoptive: 0.50; child-biological: 0.50
Answers
correlation coefficients most closely corresponds to the observed correlations between the intelligence scores of adopted children is a. child-adoptive: 0.20; child-biological: 0.40
Children for adoption
Adoption is the social, emotional, and legal process in which children who will not be raised by their birth parents become full and permanent legal members of another family while maintaining genetic and psychological connections to their birth family.
learn more about of biological here
https://brainly.com/question/14510435
#SPJ4
How do you decide which technique to use when solving an equation?
Answers
Completing the square – can be used to solve any quadratic equation. It is a very important method for rewriting a quadratic function in vertex form. Quadratic formula – is the method that is used most often for solving a quadratic equation.
What is equation?In its most basic form, an equation is a mathematical statement that indicates that two mathematical expressions are equal. 3x + 5 = 14, for example, is an equation in which 3x + 5 and 14 are two expressions separated by a 'equal' sign. A mathematical statement made up of two expressions joined by an equal sign is known as an equation. 3x - 5 = 16 is an example of an equation. We get the value of the variable x as x = 7 after solving this equation.
Here,
Any quadratic problem may be solved by completing the square. It is a critical way for expressing a quadratic function in vertex form. The quadratic formula is the most often used method for solving a quadratic problem.
To know more about equation,
https://brainly.com/question/649785
#SPJ4
please help me!!!im having so much trouble

Answers
Answer:
5 because if you do 6/3 and 10/x you would 10 times 3 then divide that by 6
2.5(2z + 5) = 5(z + 2.5)
Answers
Answer:
z is any real number
Step-by-step explanation:
2.5(2z + 5) = 5(z + 2.5)
Distribute
5z + 12.5 = 5z +12.5
Subtract 5z from each side
5z -5z + 12.5 = 5z-5z +12.5
12.5 = 12.5
This is always true so z can be any real number
Answer:
All Real Numbers
Step-by-step explanation:
We are considering the following equation - 2.5(2z + 5) = 5(z + 2.5),
\(2.5 * (2z + 5) = 5 * (z + 2.5) - Apply Distributive Property,\\\\2.5 ( 2z ) + 2.5 ( 5 ) = 5z + 5 ( 2.5 ) - Multiply Like Terms,\\5z + 12.5 = 5z + 12.5 - Subtract Terms From Either Side,\\\\0 = 0,\\Conclusion ; z - All Real Numbers\)
Solution; All Real Numbers
Answer the statistical measures and create a box and whiskers plot for the following set of data. 3,4,4,6,6,8,9,12,15
Answers
Minimum value = 3, Q1 = 4, Median = 6, Q3 = 10.5, Maximum value = 15.
Minimum value = 3
To find Q1 (the first quartile):
Arrange the data in ascending order: 3, 4, 4, 6, 6, 8, 9, 12, 15
Find the median of the lower half of the data: 3, 4, 4, 6, 6 → median = 4
Q1 is the median of the lower half of the data: Q1 = 4
Median (second quartile) = 6
To find Q3 (the third quartile):
Arrange the data in ascending order: 3, 4, 4, 6, 6, 8, 9, 12, 15
Find the median of the upper half of the data: 8, 9, 12, 15 → median = 10.5
Q3 is the median of the upper half of the data: Q3 = 10.5
Maximum value = 15
Therefore, the statistical measures for the given data set are:
Minimum value = 3, Q1 = 4, Median = 6, Q3 = 10.5, Maximum value = 15.
Learn more about median here
brainly.com/question/15545979
#SPJ4
The given question is incomplete, the complete question is:
Answer the statistical measures for the following set of data.3,4,4,6,6,8,9,12,15. Fill in the blanks. Minimum value = , Q₁ = , Median = , Q₃ = and maximum value = of the given data set.
pythagorean theorem calc: find a, b=12, c=37
Answers
Answer:
a = 35
Step-by-step explanation:
\(a^2+b^2=c^2\\a^2+12^2=37^2\\a^2+144=1369\\a^2=1225\\a=35\)
The mass of an object is x^15 grams. Its volume is x^9 cm^3. What is the object’s density?
Answers
Answer:
Step-by-step explanation:
density is mass divided by volume
15 divided by 9 is
1.6666666666
so its 1.666 repeating g/cm^3
Three numbers of the repeating decimal produced by the fraction 3/9
Answers
The repeating decimal produced by the fraction 3/9 is 0.33333..., with the digit 3 repeating infinitely.
What is fraction?A fraction is a way of expressing a part of a whole or a ratio between two quantities. It is represented as one quantity divided by another quantity, with a horizontal line called a fraction bar between them.
According to question:The fraction 3/9 can be simplified to 1/3 by dividing both the numerator and denominator by their greatest common factor, which is 3.
When we divide 1 by 3, we get a quotient of 0.3, and a remainder of 1. To continue the long division, we add a decimal point and a zero, and bring down the next digit, which is also a zero. We then divide 10 by 3, which gives us a quotient of 3, and a remainder of 1. We repeat the process, adding a decimal point and another zero, and bringing down another zero. We continue this process infinitely, getting a sequence of 3s that repeat without end.
Therefore, the repeating decimal produced by the fraction 3/9 is 0.33333..., with the digit 3 repeating infinitely.
To know more about fraction visit:
https://brainly.com/question/1301963
#SPJ1
BRAINLIEST IF YOU ANSWER THANKS!!!


Answers
ANSWER:
1. translation: 3 units right and 1 unit down
2. 130°
Solve the percent proportion. 7 is 35% of what number?
Answers
Answer:
35 ×x =7
100
35x=7
100
35x=700
35 35
x = 20.
HOPE IT HELPS,BRAINLIESTPLEASEwhich of the following sets of numbers could represent sides of a triangle?
Answers
Answer:
Hey mate...
Step-by-step explanation:
This is ur answer.....
The sum of the lengths of any two sides of a triangle must be greater than the third side. (a)(8,11,19)⇒8+11 not greater than 19 , (N.G.) (d)(13,4,8)⇒4+8<13 , (NG). Hence, option (b) is the only answer.
Hope it helps!
Brainliest pls!
Follow me! :)
which statements are true? select three options. and are parallel. and are parallel. and are perpendicular. and must intersect. lies in plane x. lies in plane x.
Answers
The true statements are, Line A B and Line C G are parallel, Line C G and Line R S are perpendicular, Line A B and Line R S must intersect and Line segment C G lies in plane X.
Given that Planes X and Y intersect at a right angle. Line AB and CG are on plane X, while line RS is on plane Y. Therefore, line CG lies on plane X.
Since both line AB and CG lie on the same plane, they are parallel to each other.
Since plane X and plane Y are perpendicular to each other and line CG is on plane X while line RS is on plane Y, this means that Line CG and Line RS are perpendicular to each other.
Line AB and Line RS may or may not intersect. They could be skew lines, which do not intersect and are not parallel.
Line segment CG lies on plane X since it is contained within the plane that contains points C, G, and either A or B.
Learn more about the parallel and perpendicular lines at
https://brainly.com/question/2188951
#SPJ4
The question is -
Which statements are true? Select three options.
a. Line A B and Line C G are parallel.
b. Line A B and Line R S are parallel.
c. Line C G and Line R S are perpendicular.
d. Line A B and Line R S must intersect.
e. Line segment C G lies in plane X.
f. Line segment R S lies in plane X.

Answer: ace
Step-by-step explanation:
What is the distance between (2,2) and (7,7)
Answers
Answer:
\(\displaystyle d = 5\sqrt{2}\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
BracketsParenthesisExponentsMultiplicationDivisionAdditionSubtractionLeft to RightAlgebra I
Coordinate Planes
Coordinates (x, y)Algebra II
Distance Formula: \(\displaystyle d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)
Step-by-step explanation:
Step 1: Define
Identify.
Point (2, 2)
Point (7, 7)
Step 2: Find distance d
Simply plug in the 2 coordinates into the distance formula to find distance d.
Substitute in points [Distance Formula]: \(\displaystyle d = \sqrt{(7 - 2)^2 + (7 - 2)^2}\)[Order of Operations] Evaluate: \(\displaystyle d = 5\sqrt{2}\)LarCalc11 9.4.023. Use the Limit Comparison Test to determine the convergence or divergence of the series. S- n v n8 + 9 n = 1 n v n8 + 9 = L >O him 1 lim n >0 =230 O converges O diverges Need Help? Read It Watch It Talk to a Tutor Viewing Saved Work Revert to Last Response Submit Answer Practice Another Version
Answers
The series in question is given by S_n = √(n^8 + 9n). The ratio of the terms approaches a finite positive value. We want to determine whether this series converges or diverges using the Limit Comparison Test.
1. To apply the Limit Comparison Test, we choose a known convergent series with positive terms, let's call it b_n. In this case, we can choose b_n = √(n^8).
2. Now, we need to find the limit of the ratio of the terms of the two series as n approaches infinity. We calculate the limit:
lim n→∞ (√(n^8 + 9n) / √(n^8))
Simplifying the expression inside the limit, we have:
lim n→∞ (√(n^8 * (1 + 9/n)) / n^4)
3. Using properties of limits, we can rewrite the expression as:
lim n→∞ (√(n^8) * √(1 + 9/n) / n^4)
Simplifying further, we have: lim n→∞ (n^4 * √(1 + 9/n) / n^4)
4. The n^4 terms cancel out, leaving us with: lim n→∞ √(1 + 9/n)
As n approaches infinity, the term 9/n approaches zero, and we are left with: lim n→∞ √1 = 1
5. Since the limit is finite and positive (L = 1), and the series b_n = √(n^8) converges, we conclude that the original series S_n = √(n^8 + 9n) also converges.
6. In summary, using the Limit Comparison Test, we determined that the series S_n = √(n^8 + 9n) converges. The explanation above shows the step-by-step calculation of the limit, demonstrating that the ratio of the terms approaches a finite positive value.
Learn more about Limit Comparison Test here: brainly.com/question/31362838
#SPJ11
Is the following number rational or irrational? sqrt(50) Choose 1 answer ?
Answers
Answer:
its irrational
7.07106781187
look at how the decimals are all over the place
if it was rational it would've been something like this
7.070707070707 or 7.071071071071
hope that answers your question
Step-by-step explanation:
Which of the following is the correct factorization of the polynomial below?
x3 + 10x2 + 25x
A. x(x + 5)(x - 5)
B. (x2 + 2x - 5)(x-10)
C. (x2 + 5x - 2)(x-10)
D. x(x + 5)2
Answers
Answer:
x(x+5)^2
Step-by-step explanation:
x^3 + 10x^2 + 25x
Factor out x
x(x^2+10x+25)
What 2 numbers multiply to 25 and add to 10
5*5 = 25
5+5 =10
x(x+5)(x+5)
x(x+5)^2
Answer:
D
Step-by-step explanation:
Given
x³ + 10x² + 25x ← factor out x from each term
= x(x² + 10x + 25) ← perfect square
= x(x + 5)²
which expression is equivalent to the given expression?

Answers
Answer:
4ln x +ln 3-lnx
4ln x -ln x+ln3
3ln x+ln 3
ln(3x+3)is equivalent.
find the mean of the data set 2 9 7 4 6 1
Answers
Answer:
i think its six i haven't done this in a while tho
Step-by-step explanation:
sort them in order from least to greatest and find the middle... i think... that could be medium
Answer:
Step-by-step explanation:
The mean is the average so add them all up and divide the sum by the amount of number there are \(2+9+7+4+6+1=29\) and then divide 29÷6 = 4.8333333333 (3 continued) or 29/6 (fraction) also if that is not the answer round it and it would be 4.8
8. Based on data from the National Health Board, weights of men are normally distributed with a mean of 178 lbs, and a standard deviation of 26 lbs. Find the probability that 20 randomly selected men will have a mean weight between 170 and 185. [3]
Answers
The probability that the mean weight of 20 randomly selected men is between 170 and 185 lbs is approximately 0.7189 or approximately 72%.
To solve this problem, we need to use the formula for the sampling distribution of the mean, which states that the mean of a sample of size n drawn from a population with mean μ and standard deviation σ is normally distributed with a mean of μ and a standard deviation of σ/sqrt(n).
In this case, we have a population of men with a mean weight of 178 lbs and a standard deviation of 26 lbs. We want to know the probability that 20 randomly selected men will have a mean weight between 170 and 185 lbs.
First, we need to calculate the standard deviation of the sampling distribution of the mean. Since we are taking a sample of size 20, the standard deviation of the sampling distribution is:
σ/sqrt(n) = 26/sqrt(20) = 5.82
Next, we need to standardize the interval between 170 and 185 lbs using the formula:
z = (x - μ) / (σ/sqrt(n))
For x = 170 lbs:
z = (170 - 178) / 5.82 = -1.37
For x = 185 lbs:
z = (185 - 178) / 5.82 = 1.20
Now we can use a standard normal distribution table (or a calculator) to find the probability of the interval between -1.37 and 1.20:
P(-1.37 < z < 1.20) = 0.8042 - 0.0853 = 0.7189
Therefore, the probability that 20 randomly selected men will have a mean weight between 170 and 185 lbs is 0.7189 or approximately 72%.
Learn more about standard deviation at https://brainly.com/question/475676
#SPJ11
How do you remember greater than less than?
Answers
The usual sign for greater than and less than is "<", the pointed side is always towards the smaller quantity.
When we compare two quantities in mathematics we us the sign"<".
Now, let us say that there are two quantities a and b, and a is greater than b. So, we can write the relation as, a > b. So, we see that b is less than as a and a is greater than b.
Now, to remember this, the pointed side of the sign will be always towards the quantity that is smaller.
To know more about greater than less than, visit,
https://brainly.com/question/713540
#SPJ4
The length l of a rectangle is decreasing at the rate of 2 cm/sec while the width w is increasing at the rate of 2 cm/sec. When l = 12 cm and w = 5 cm, find the rates of change of (a) the area, (b) the perimeter, and (c) the lengths of the diagonals of the rectangle. Which of these quantities are decreasing, and which are increasing?
Answers
Using Area and perimeter formulae of rectangle,
a) the rate of change of Area is 14 cm²/sec
b) the rate of change of perimeter is zero.
c) length of diagonal is 13 cm
We have given that
length (l) is decreasing at the rate of 2 cm/min
and the width (w) is increasing at the rate of
2cm/min,
⇒ dl/dt = −2 cm/min and dw/dt = 2cm/sse
Thus the perimeter (P) of a rectangle is,
P=2(l+w) ---(1)
differentiating above equation with respect to time (t) we get,
dp/dt = 2(dl/dt + dw/dt )
=> dp/dt = 2( -2 + 2 ) = 0
=> P = constant
Hence, there is no change in perimeter of rectangle.
(b)Now, it is given that length (l) is decreasing at the rate of 2 cm/min
and the width (w) is increasing at the rate of 2 cm/min,
Thus the area (A) of a rectangle is, A= l× w
=> dA/dt = l ×dw/dt + w×dl/dt (used differentaion
we have l = 12 cm and w = 5 cm
=> dA/dt = 12 (2) + 5(-2)
=> dA/dt = 24 - 10 = 14
Hence, the area is increasing at the rate of
14 cm²/min.
c) length of diagonal = √(12)² + (5)² = √144+25
=> length of diagonal = √169 = 13 cm
To learn more about Rate of change of area , refer:
https://brainly.com/question/13946172
#SPJ4
Help me asp 25 points and will mark

Answers
Answer:
Slope = - 2
Step-by-step explanation:
Given equation is,
y= - 2x
If x=1, y= -2.
If x=2, y= - 4
Take such few points and plot the graph (1, - 2), (2, - 4)........
Draw a straight line through the points.
For slope, compare the equation with slope intercept form, y=mx + c
Here, c=0 and m=-2
Hope this helps!!
Write an expression for the calculation triple 4 and then add 6 times 6
Answers
Answer:
4x3+6x6=48
Step-by-step explanation:
PEMDAS
4x3=12
6x6=36
12+36=48
therefore, the answer is 48
x+y+z= 232
y = 32 - 4
y +z = x
Answers
Answer:
x=166 , y=28 , z=88
Step-by-step explanation:
Please help me this is my last question
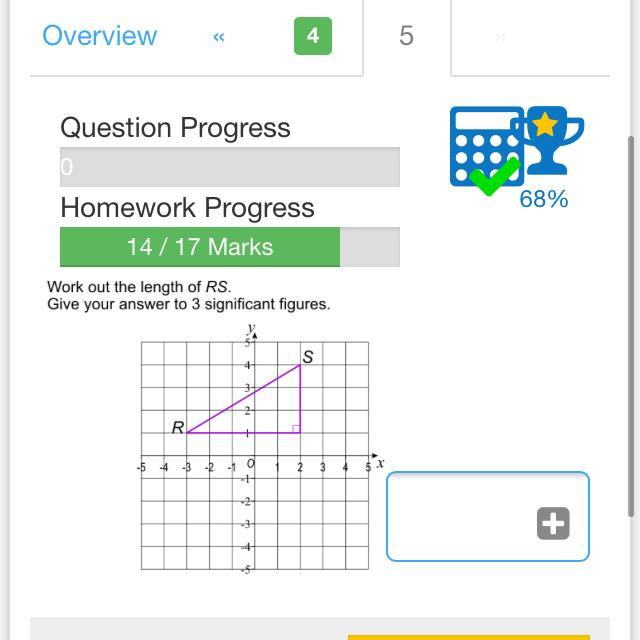
Answers
Answer:
5.831
Step-by-step explanation:
Pythagoras says RS = √(5²+3²) = √34 ≈ 5.831
Answer:
RS ≈ 5.83 units
Step-by-step explanation:
Using Pythagoras' identity in the right triangle.
The square on the hypotenuse is equal to the sum of the squares on the other 2 sides.
Here RS is the hypotenuse and the legs have measure 5 and 3, thus
RS² = 5² + 3² = 25 + 9 = 34 ( take the square root of both sides )
RS = \(\sqrt{34}\) ≈ 5.83 ( to 3 significant figures )
If in a population of 100 individuals, the allele frequency of the dominant allele is 0.8, how many homozygous dominant individuals are there? a. 64 b. 32 c. 16 d. 80
Answers
The answer is 64. To find the number of homozygous dominant individuals in the population.
We need to use the Hardy-Weinberg equation:
p^2 + 2pq + q^2 = 1
Where:
p = frequency of dominant allele
q = frequency of recessive allele
Since the dominant allele frequency is 0.8, we can assume that the recessive allele frequency is 0.2 (since p + q = 1).
To find the frequency of homozygous dominant individuals (p^2), we simply square the frequency of the dominant allele:
p^2 = (0.8)^2 = 0.64
To find the number of homozygous dominant individuals, we multiply the frequency by the total population size:
0.64 x 100 = 64
Therefore, there are 64 homozygous dominant individuals in the population.
Learn more about dominant here:
https://brainly.com/question/30418951
#SPJ11
9 x 10^2 is how many times as much as 3 x 10^-2?
Answers
Answer:3*10^4
Step-by-step explanation:
3 multiply 10 to the 4 power (positive)